Tsunamis durch Asteroideneinschlag

Da 70% der Erdoberfläche von Wasser bedeckt sind, unter Annahme, dass die Einschläge gleichmäßig über die Erdoberfläche verteilt sind, sind die Chancen, dass der Asteroid ins Wasser fällt viel höher, als ein Einschlag an Land. Was geschieht in diesem Fall? Was für Schäden werden angerichtet? Wie unterscheiden sie sich von den Auswirkungen, die ein auf Land eingeschlagener Asteroid hat?
Die University of California, Santa Cruz hat eine Simulation berechnet mit dem Asteroiden 1950DA, der 1950 entdeckt und daraufhin 17 Tage lang beobachtet wurde, dann aus den Augen verloren und erst am Sylvesterabend 2000 wieder gesehen wurde. Aus den Daten von 1950 und neuen Messungen mit Hochpräzisionsradar konnte Position (±0,9 km) und Geschwindigkeit (± 3,5 cm/s) bestimmt werden. Aus Extrapolationen der Bahn ergibt sich eine Wahrscheinlichkeit eines Einschlags von 0,0 bis 0,3 % auf der Erde am 16. März 2880. bei der der Asteroid, ein Felsbrocken von einem 1.1 Kilometer Durchmesser, einer Masse von 1,55 *10^12 kg mit einer Geschwindigkeit von 60 000 km/h in den Atlantik vor die Küste der USA fällt. Eine Besonderheit hat er auch: er dreht sich mit einer Periode von 2,1 Stunde, der zweit höchsten bekannten Umdrehungsgeschwindigkeit eines Asteroiden
Solche Extrapolationen über mehr als 800 Jahre sind natürlich sehr unsicher, viele Einflüsse (Störungen durch Planeten und andere Asteroiden, sichtbare und unsichtbare, Kollisionen mit kleineren Asteroiden, Jarkovsky Effekt.) können die Bahn noch stark ändern.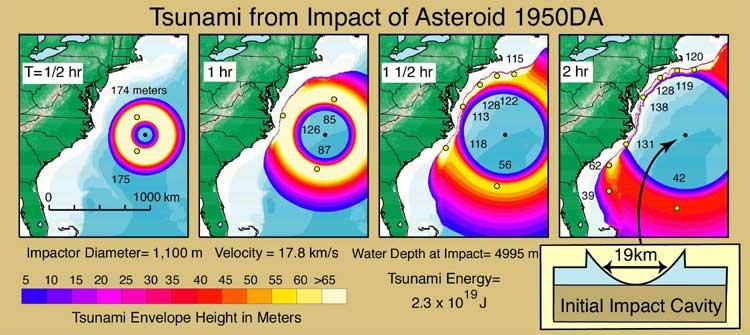

Die Simulation wurde nach der klassischen Theorie von Wasserwellen mit Anfangsbedingungen (Ozeantiefe, Anfangsauslenkung und Geschwindigkeit) berechnet. Die angeregten Wellenkomponenten bleiben nicht lange zusammen, da die niedrigfrequenten Wellen schneller sind als die hochfrequenten, und diese überholen. Daher wurde mit der einhüllenden Funktion modelliert, daraus kann auch die Energie des Einschlags abgeleitet werden. Die Ergebnisse der Berechnungen sind die kinetische Energie (M=1,55*10^12kg und v= 60 000 km/h ) ½mv² = 2,46*10^20 Joule. Davon wird nur ein kleiner Teil , nämlich 9,4% in Tsunamis umgesetzt. An der Küste die am nähesten liegt, entstehen Wellen von bis zu 120m Höhe, etwas weiter weg, 4 bis 5 Stunden später 60 Meter hohe Wellen. Je nach Art der Küste und Entfernung haben die Wellen verschiedene Formen und Wellenlängen.
In der Karibik sind die Wellen nur noch 30-35m hoch, Kuba und andere Inseln schirmen Teile der Küste von Südamerika ab.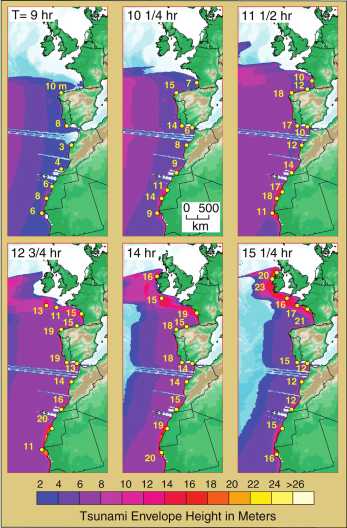

8 Stunden nach dem Einschlag erreichen die ersten Wellen Afrika und Europa, wo dann 6 Stunden lang Wellen von 10-15m Höhe auftreffen.Die britischen Inseln werden etwas später getroffen und schirmen die Küste von Belgien, Holland, Deutschland und Dänemark ab.
Am Meeresboden bewegen sich Bodenwellen mit einer Geschwindigkeit von 1m/s bis 800 km/s Die Erschütterungen am Boden lösen Erdbewegungen aus, es kommt zu Seebeben und weiteren Tsunamis. Das ist ein typisches Szenario für einen eingeschlagenen Asteroiden dieser Größe. Solche Einschläge haben in der Erdgeschichte ziemlich sicher schon mehrmals stattgefunden.
(Grafiken: University of California, Santa Cruz)